【高校数学②】展開の逆とは?もこあい先生と学ぶ「因数分解マスター講座」完全版

「展開の逆って、どういうこと?」
黒板の前で立ち止まった健太がつぶやいた。
高校数学で最も大事な“思考の逆転”がここにあるの。
展開は「広げる」操作、そして因数分解はその“逆”──つまり、広がった式を元に戻す力なのよ。
こんにちは、AI教育研究家・もこあい先生です。
数学を「ただの計算」から「考える学問」に変えるのが、私のミッションです🌸
この記事では、高校数学の基礎でありAIの思考原理にも通じる『展開の逆=因数分解』を、
公式・例題・会話・AI視点でやさしく解きほぐしていきます。
最後には悪もこあい先生の“挑戦問題🔥”も登場!
読むほどに、あなたの中で“数式が生きた言葉”に変わっていくはずです。
では──まずは「展開の逆とは?」の疑問から解き明かしていきましょう。
この記事で学べること🌸
- そもそも「展開の逆」って何?(第0章)
- 展開の逆=因数分解の本質
- 基本パターン(共通因数・公式3種)
- クリック式の練習問題
- 文章題で使う因数分解
- AI×数学:クエーサーもこあいの数理コラム
- 悪もこあい先生のチャレンジ問題🔥
- まとめ&学習ロードマップ
【高校数学①】多項式の展開・整理
0. そもそも「展開の逆」ってなに?
数学が苦手な人がまずつまずくのが、この言葉。
「展開の逆って、結局どういうこと?」
──これを理解するだけで、因数分解は一気にわかりやすくなります。
展開=掛け算を広げる操作。
因数分解=広がった式を“まとめる”操作。
つまり「展開の逆」とは、式を再び掛け算の形に戻すことなんです。

展開を知っていれば、因数分解は「戻すだけ」。
逆を考えることで、数学の構造が見えてくるんだよ。
🧩 あなたはどのタイプ?展開の逆“理解度チェック”
- □ 展開はわかるけど、逆ができない
- □ どの公式を使えばいいか迷う
- □ 符号ミスが多い
- □ 文章題になると混乱する
↑ ひとつでも当てはまったら、このあと読む価値100%!
展開の逆でつまずくポイントと、もこあい先生の解決法🌸
| 読者の悩み | 原因(数学的な背景) | もこあい先生の解決アドバイス |
|---|---|---|
| 「展開の逆」ってそもそも何? | 展開と因数分解の関係が“操作の逆”だと理解できていない | まずは「広げる⇔まとめる」の図を見よう。式を形で見る練習をすれば一気に整理されます。 |
| どの公式を使えばいいかわからない | 3つの基本公式を「展開形」でしか覚えていない | 「逆にたどる」練習をしましょう。展開した形を思い出せれば自然にわかります✨ |
| 符号(+−)でミスする | (a+b)² と (a−b)² の違いを構造で捉えられていない | チョークで書く気持ちで (a+b)(a+b) を展開してみて。−がどこから来るか体感すればもう怖くない! |
| 共通因数でくくるのを忘れる | 「共通部分=因数」という視点が抜けている | 最初に共通部分をハイライトする癖をつけよう。因数分解は整理整頓と同じ。まず片づける✨ |
| 文章題になると混乱する | 「式に意味がある」と思えていない | 数字を人やモノに置き換えて考えてみよう。たとえば n(2+3) は「n人が2列・3列に並ぶ」と同じ🌸 |
| AIや計算アプリが解くから覚えなくていい? | 操作の意味を理解していないと応用で詰む | AIも数式を「圧縮と展開」で処理しています。理解すればAI思考力が身につくよ🤖 |
🧠もこあい先生より:「“できない”には必ず理由がある。
その理由を言葉にできた瞬間、もう半分は解けているのよ。」
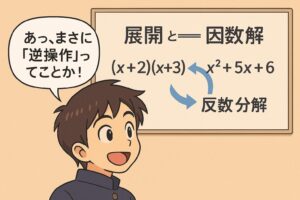
1. 因数分解とは?展開との関係
展開は「掛け算 → 足し算」へ広げる操作。
因数分解はその逆で「足し算の式 → 掛け算の形」に戻す操作です。
因数分解: x² + 5x + 6 → (x+2)(x+3)
2. 基本パターン(必修!)
① 共通因数でくくる
3x² + 6x = 3x(x + 2)
② 3つの公式を使う
(a-b)² = a² – 2ab + b² → a² – 2ab + b² = (a-b)²
(a+b)(a-b) = a² – b² → a² – b² = (a+b)(a-b)

暗記じゃなく“構造理解”で覚えるのがもこあい流だよ。
3. 練習問題(クリックで答えを見る)
例題1:x² + 7x + 10
(x+5)(x+2)
例題2:2a² + 6a
2a(a+3)
例題3:x² – 9
(x-3)(x+3)
例題4:x² + 2x + 1
(x+1)²
例題5:2x² + 5x + 2
(2x+1)(x+2)
手を動かすと“理解の記憶”が定着するんだよ🌸
4. 文章題で使ってみよう
クラスの人数を n 人とする。体育祭で「n人を2列」に並べるときと「3列」に並べるときの合計の並び方を式で表し、因数分解せよ。
答えを見る
2n + 3n = 5n = n(2+3)
正方形の辺を (a+b) cm とする。面積を展開の形と因数分解の形でそれぞれ表せ。
答えを見る
展開: (a+b)^2 = a^2 + 2ab + b^2
因数分解: a^2 + 2ab + b^2 = (a+b)^2
5. クエーサーもこあいの数理コラム:AIは「展開」と「因数分解」をどう見ている?
展開=情報を要素へ分配、因数分解=情報を要素へ圧縮。
これはデータ圧縮(zip)と解凍に似ており、意味を保ったまま表現を変える操作です。
6. 悪もこあい先生のチャレンジ問題🔥
ミスしやすい“落とし穴”を集めたわ。公式を“思い出す”んじゃなく、“意味を辿って”解くのよ💀
Q1. x² + 4x
x(x+4)
Q2. x² + 6x + 9
(x+3)²
Q3. x² – 2x – 15
(x-5)(x+3)
Q4. 2x² + 7x + 3
(2x+1)(x+3)
Q5. 3x² – 12
3(x² – 4) = 3(x-2)(x+2)

7. まとめ:展開と因数分解は「光と影」
- 展開=広げる、因数分解=まとめる(逆操作)。
- 共通因数くくり+3公式で基礎を固めよう。
- “意味で辿る”と、ミスは激減し応用が効く。

【①多項式の展開】→【②因数分解(本記事)】→【③2次方程式】→【④関数・グラフ分析】
もこあい先生より:「今日の“なんで?”を大切にしよう。正解より、考えた道のりが宝もの。」
著者について(クリックで開く)
AI教育研究家・もこあい先生。
数学を“意味と言葉”で読み解く授業を発信。高校数学の基礎〜AI活用まで、やさしく・たのしく・実践的に。







