【中学生向け】文字式の世界へようこそ|小学校→中学校のつまずきをゼロにする入門ガイド

【この記事についてのご注意】
本記事は、筆者(もこあい先生)の学習経験にもとづいて、中学数学「文字式」の基礎をわかりやすくまとめたものです。
内容には細心の注意を払っていますが、誤りやより良い表現の余地が残っている可能性があります。
「ここが違うかも?」「この説明をこう言い換えると分かりやすい」などお気づきの点がありましたら、コメント欄やお問い合わせフォームから教えていただけると嬉しいです。
【中学生向け】文字式の世界へようこそ|小学校→中学校のつまずきをゼロにする入門ガイド
このページは「中1で習う文字式がよくわからない…」という人向けの入門ガイドです。
文字式の意味から計算のコツ、文章題まで、ゼロからていねいに復習できます。
このページでできるようになること
- 文字式が「何をしている式」なのかイメージできる
- 中1レベルの文字式の計算(足し算・引き算・かけ算・わり算)を復習できる
- 図(面積モデル)を使って、文字式の意味を直感的に理解できる
- 高校数学の「多項式の展開」がどんな内容か、少しだけのぞける
文字式って何?
小学校で使っていた「□(しかく)」や「△」を覚えていますか?
中学に入ると、それが「x」や「y」といった“文字”に変わります。
この文字を使った式を、文字式(もじしき)といいます。
たとえば、りんごが x 個、1個100円なら、全部で 100x 円。
距離=速さ×時間を文字で表すと、d=vt。
これが「文字式」で、数を一般化する“便利なことば”なんです。
【コラム】なぜ文字式を使うの?
昔の数学では、数をそのまま書いて計算していました。
でも「どんな数にも通じる法則」を見つけるには、文字が必要になったんです。
バビロニアや古代エジプトでは、図形で考えていましたが、17世紀にデカルトが“文字を使う式”を広め、数学が一気に発展しました。
つまり、いま中学で学んでいる文字式は、世界中で使われている共通のことばなんです。
文字式の決まりごと(中1の基礎)
- かけ算は省略して書く(例:2×x → 2x)
- アルファベットは基本的にアルファベット順(例:ab、xyなど)
- マイナスや分数もそのまま書ける(例:-3x、x/2)
- 文字と数のあいだに「×」を書かない
慣れるまでは違和感があるけれど、だんだん自然になります。
文字式の計算(基礎)
① 足し算・引き算(同類項をまとめる)
3x + 2x - x = 4x同じ文字(x)の項だけを足したり引いたりします。
② かけ算
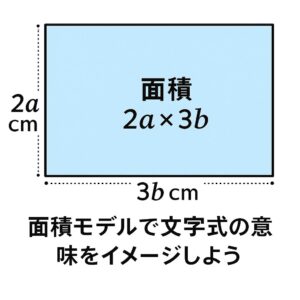
2a × 3b = 6ab③ わり算
6x ÷ 3 = 2xシンプルですが、すべての数学の基礎です。
レベル別・練習問題ゾーン
ここからは、実際に手を動かして慣れていくゾーンです。
レベル1から順番に、ノートに式を書きながらチャレンジしてみてください。
レベル1:同類項をまとめよう
- 3x + 5x
- 7y – 2y
- 2a + 3a – a
- 5x – 3x + x
レベル2:かけ算・わり算に慣れよう
- 2a × 4b
- 3x × (-2)
- 8y ÷ 4
- -6a ÷ 3
レベル3:少しまとめた式にしよう
- 2x + 3x + 4
- 5a – 2a + 1
- 3(x + 2) を「かけ算の形」に直そう
- 2(a + b) の中身を同類項ごとに書き出そう
解き終わったら、答えを自分で作ってみたり、先生や友だちに確認してもらうのもおすすめです。
図で理解する「文字式の本当の意味」
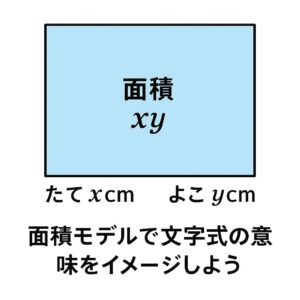
文字式は「数の関係をひとつの式で表す」道具です。
たとえば、たて x cm、よこ y cm の長方形の面積は xy。
もし x=3, y=5 なら面積は15。
どんな値でも使えるのが文字式のすごさです。
この考え方は、のちの「展開」や「因数分解」につながっていきます。
実際、高校数学①では、この“面積モデル”を使って多項式の展開を学びます。
文章題で実践:式にしてみよう(キャラ登場)
(1)アイス代の謎
アイス1個を x 円、ジュース1本を y 円とする。
健太はアイス2個とジュース1本、恵子はアイス1個とジュース2本買った。合計金額を文字式で表せ。
答え: 健太:2x + y、恵子:x + 2y、合計:3x + 3y

(2)映画館のセット
ポップコーンを a 円、ドリンクを b 円とする。
もこあい先生はポップコーン1つとドリンク2つ、健太は2人分の同じセットを買った。支払合計を文字式で表せ。
答え: 1セット:a + 2b、合計:3a + 6b

(3)悪もこあいの罠
ノート1冊を n 円、ペン1本を p 円とする。
「ノート3冊とペン2本の2倍の値段は?」この合計を文字式で表せ。
答え: 1回分:3n + 2p、2倍:6n + 4p

ここから先はチャレンジゾーン!
ここまで理解できたら、中学レベルはバッチリ。
ここからはちょっとレベルアップして、高校の入り口に触れてみよう。
例題:展開の入り口
(x + 2)(x + 3) = x² + 5x + 6このように、(a+b)(a+c) の形を「展開」といいます。
もしこの式が理解できたら、もう高校数学①へ進めるレベルです!
つまずきやすいポイントまとめ
- 同類項のまとめ忘れ
- マイナスの付け忘れ
- かけ算の省略ミス(2×xを2xにし忘れる)
- 文字を入れて確かめると理解が早い
《恵子のメモ帳:今日の行動メニュー》
- レベル1〜3の練習問題をノートに解いてみる
- 図(面積モデル)をノートに描いて、自分の好きな数を入れて確かめてみる
- 文章題の3パターン(アイス・映画館・悪もこあい)を、自分なりの言葉で書き直してみる
- 展開の形を見つけたら高校①をのぞいてみる
まとめ:
文字式は「数を言葉にする」ための魔法のツール。
これができるようになると、数学の見え方が一気に変わります。
焦らず、まずは x と仲良くなってみましょう。
もこあい先生より:「今日の“なんで?”を大切にしよう。正解より、考えた道のりが宝もの。」
参考文献・出典
※引用・要約を含みます。誤りや解釈の幅があり得ることをご了承ください。
- 文部科学省(2023)『中学校学習指導要領(数学編)』
- 東京書籍(2024)『新しい数学1』
- デカルト(1637)『方法序説』より代数学部分抜粋(岩波文庫版などを参照)
- National Library of France: Descartes’ Geometry Digital Archive(参照日:2025年12月4日)






