【高校数学①】多項式の展開をゼロから理解する｜中学→高校へのつまずきが消える入門ガイド

こんにちは、もこあい先生です。
このページは、わたしのブログで始まる「高校数学シリーズ」の1本目として書いています。

「(a+b)²＝a²＋2ab＋b²」
高校の授業で黒板にこの式が出てきた瞬間、
「あ、これもう無理かも…」と感じた人もいるかもしれません。
でも、心配しなくて大丈夫。
“わからない側の気持ち”に立って、ゼロから一緒にやり直すための記事にしてあります。

もしあなたが、先にこちらの中学生記事

【中学生向け】文字式の世界へようこそ｜小学校→中学校のつまずきをゼロにする入門ガイド

を読んでくれていたら、ここはその「続きの授業」にあたります。
もちろん、まだ読んでいなくても大丈夫。この記事だけで分かるように作ってあるので、あとからゆっくり戻ってもらえればOKです。

この高校数学シリーズでは、もこあい先生として次のことを約束します。

• 中学→高校でどこでつまずきやすいかを、ちゃんと言葉にすること
• 公式を丸暗記させるだけの授業にはしないこと
• 図・たとえ話・キャラクターを使って、「できる」まで伴走すること

そのうえで、この記事では次の流れで進みます。

• ① 中学の文字式・算数の「ほんの少しのモヤモヤ」を言語化する
• ② (a+b)²・(a−b)²・(a+b)(a−b) を図形（面積）から理解する
• ③ 数字の例題や小テストで、「わかる」から「できる」に変える

「高校数学、今からでも間に合う？」
——はい、大丈夫です。
ここでは、途中で数学が苦手になった人も、これから学び直したい大人も、
みんながもう一度スタートラインに立てるように、ゆっくり・ていねいに進めていきます。

1．高校数学でいきなりつまずく理由は「構造のジャンプ」

ここからは、教室でもこあい先生が黒板の前に立って話しているイメージで読んでみてください。

中学までの数学（算数を含めて）は、こんな感覚でも何とかなった人が多いと思います。

• とりあえず計算のやり方を覚える
• パターンに当てはめて、形をマネする
• 答えが合えばOK

一方、高校数学からは「なぜその式になるのか」「この式は何を表しているのか」といった
構造そのものを理解していないと、すぐに行き詰まります。

多項式の展開は、その最初の「ジャンプするポイント」です。ここで

• 公式を暗記して乗り切る → 後で苦しくなりがち
• 意味から理解する → その後の数学が一気にやさしくなる

という分かれ道が生まれます。

2．高校数学の前に：算数の「4つの基礎」をそっと思い出す

◆ 健太コラム：「じつは算数からちょっと自信がなくて…」

高校数学の「展開公式」につまずいている人の多くは、
実はその手前、算数〜中学数学の次の4つがモヤっとしていることが多いです。

1. ① 分配法則：a(b+c)=ab+ac
2. ② かっこの意味：「ひと固まり」として扱う感覚
3. ③ 割り算の意味：等分・逆数としてのイメージ
4. ④ 面積で考える力：縦×横＝四角形の面積

この記事では、これらを「できるだけ自然に」思い出しながら進みます。
完璧じゃなくて大丈夫。
読んでいるうちに「あ、そうだった」とつながればそれでOKです。

3．そもそも「多項式」って何？中学の文字式とのつながり

まずは言葉の整理からいきましょう。
中学で扱っていたものは、だいたいこんな感じでした。

• x＋3
• 2x−5
• 3x＋4y

これらは、中学では「文字式」と呼ばれていました。
高校になると、これらは「多項式」というグループの中に入ります。

ざっくり言えば、

• 項が1つ：単項式（例：2x、−5a²）
• 項が2つ以上：多項式（例：x＋3、2x−5、3x＋4y）

というイメージで大丈夫です。
「多項式の展開」というのは、
かけ算の形になっている多項式を、足し算・引き算の形に広げていくことだと思ってください。

4．展開って具体的に何をしているの？

次の式を見てみましょう。

(x+2)(x+3)

これは、

• 「x＋2」という箱
• 「x＋3」という箱

をかけ算しているイメージです。
このとき、中身同士を全部かけ合わせると、

(x+2)(x+3)
= x(x+3) + 2(x+3)     ← 分配法則
= x²+3x + 2x+6
= x²+5x+6

ここで使っているのが、さっき出てきた
「分配法則 a(b+c)=ab+ac」です。

展開とは、分配法則を徹底的に使って、かけ算の形を「広げる」操作。
これを図形で見ると、もっとスッキリ分かるようになります。

5．図形で理解する (a+b)²：面積から生まれる展開公式

まずは、有名な

(a+b)² = a² + 2ab + b²

を、図（面積）から理解してみましょう。

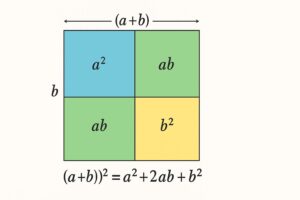
一辺が「a+b」の正方形を考えます。
横方向を「a」と「b」に分け、縦方向も同じように「a」と「b」に分けると、
中は4つの長方形（または正方形）に分かれます。

• 左上：縦a × 横a → a²
• 右上：縦a × 横b → ab
• 左下：縦b × 横a → ab
• 右下：縦b × 横b → b²

正方形全体の面積は、4つの面積を足したものなので、

(a+b)² = a² + ab + ab + b²
        = a² + 2ab + b²

となります。
これがそのまま、あの有名な公式の「意味」です。

6．(a−b)² と (a+b)(a−b) も面積でわかる

6-1．(a−b)²：なぜ「−2ab」になるの？

つぎに

(a−b)² = a² − 2ab + b²

を同じように面積で考えてみましょう。

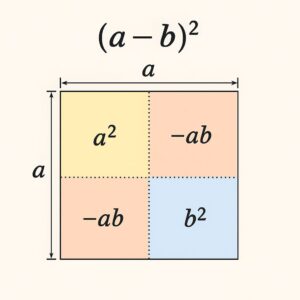
もともと「一辺 a の正方形」があったと考えます。
そこから「幅 b の帯」を2本引き抜き、最後に「b² の小さな正方形」を戻すイメージです。

• もとの面積：a²
• 横方向の帯：ab を1つ引く
• 縦方向の帯：ab をもう1つ引く
• 引きすぎた角の部分：b² を足し戻す

よって、

(a−b)² = a² − ab − ab + b²
        = a² − 2ab + b²

となります。
「−2ab」のところには、「帯を2本引いた」という意味があるわけです。

6-2．(a+b)(a−b)：なぜ「真ん中の項」が消えて a²−b² になるの？

最後に、

(a+b)(a−b) = a² − b²

を図で見てみましょう。

(a+b)(a−b) を展開すると、

(a+b)(a−b)
= a(a−b) + b(a−b)
= a² − ab + ab − b²

真ん中の「−ab」と「+ab」がちょうど打ち消し合うので、

(a+b)(a−b) = a² − b²

となります。
図でも、真ん中の部分が「プラスとマイナスで打ち消される」形になっているのが分かります。

7．数字で確かめる：(5+2)² を図と計算でつなげる

ここまで「文字 a, b」で考えてきましたが、
数字で一度確認すると、さらに理解が深まります。

一辺が 5+2 = 7cm の正方形を考えます。すると面積は 7² = 49 です。
これを、5cm の部分と 2cm の部分に分けてみると、

• 5×5 = 25
• 5×2 = 10
• 2×5 = 10
• 2×2 = 4

4つの面積を足すと、

25 + 10 + 10 + 4 = 49

となり、

(5+2)² = 5² + 2×5×2 + 2²
       = 25 + 20 + 4
       = 49

という形で、(a+b)² の公式とぴったり対応していることがわかります。

8．「広がる」と「収束する」：展開と因数分解のイメージ

ここまで見てきたように、

• 展開：かけ算の形 → 足し算・引き算の形へ広げる操作
• 因数分解：足し算・引き算の形 → かけ算の形へまとめる操作

という関係があります。
これは、考え方の「広がる」と「収束する」にもよく似ています。

まずは「どうなっているんだろう？」と、いろいろな方向へ考えを広げる。
そして最後に、「結局いちばん大事なところは何か？」と、考えを収束させていく。
展開と因数分解は、まさにこの行き来を数式でやっているようなものです。

だから、

• 展開を理解する
• 因数分解へつなげる

という流れをしっかり押さえておくと、
これから学ぶ二次関数・グラフ・方程式の世界がぐっと見通しよくなります。

9．健太の小テスト：自分でもやってみよう

最後に、「分かったつもり」から「実際にできる」に変えるためのミニテストです。
健太と一緒に解いてみましょう。

時間がない日は、問1だけでもOKです。
「ノートに図を1つ写す＋問1を解く」だけでも、かなり定着します。

問1：基本の展開

1. (x+3)² を展開せよ。
2. (2x−5)² を展開せよ。

問2：(a+b)(a−b) 型

3. (x+4)(x−4) を展開せよ。
4. (3a+2)(3a−2) を展開せよ。

問3：少しだけ応用

5. (2x+1)² を展開しなさい。
6. (x−1)(x−2) を展開しなさい。

(x+3)²
= x² + 2×x×3 + 3²
= x² + 6x + 9

(2x−5)²
= (2x)² − 2×2x×5 + 5²
= 4x² − 20x + 25

(x+4)(x−4)
= x² − 4²
= x² − 16

(3a+2)(3a−2)
= (3a)² − 2²
= 9a² − 4

(2x+1)²
= (2x)² + 2×2x×1 + 1²
= 4x² + 4x + 1

(x−1)(x−2)
= x(x−2) − 1(x−2)
= x² − 2x − x + 2
= x² − 3x + 2

10．今日のまとめ：展開は「意味が分かれば一生モノ」

ここまで読んでくれてありがとう。
最後に、今日の授業で押さえておきたいポイントを、もこあい先生目線でぎゅっとまとめます。

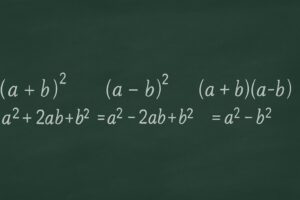
今日のポイントは、次のとおりです。

• 展開は分配法則を徹底して使う操作
• (a+b)² の意味は、正方形の面積を4つに分けた図で理解できる
• (a−b)² の「−2ab」は「帯を2本引いた」イメージ
• (a+b)(a−b)=a²−b² は、真ん中の項がきれいに打ち消し合う仕組み
• 数字の例（(5+2)²など）で確かめると、公式と図形がつながる
• 展開と因数分解は「広がる ↔ 収束する」考え方のペアになっている

訂正と追記

この記事の内容は、定期的に見直し・追記を行っています。
新しい説明方法や、より分かりやすい図解が思いついたときは、随時アップデートします。

• 2025-11-26：初公開版を掲載。
• 今後、読者の声やご指摘をもとに、例題や図を追加する予定です。

もし誤りや分かりにくい箇所を見つけた場合は、
コメント欄またはお問い合わせフォームから教えていただけると助かります。

参考文献・出典（数学記事用）