【高校数学③】もこあい先生と学ぶ2次方程式|因数分解・平方完成・解の公式を「選べる」ようになる授業

二次方程式は、「3つの解法をどう使い分けるか」がわかると、一気にラクになります。
この記事では、因数分解・平方完成・解の公式を、もこあい先生たちと一緒に「選べる」ようになるところまで丁寧に解説します。
※この記事について
高校数学Iレベルの2次方程式を対象にしています。
学校の教科書・授業内容に沿った一般的な解説をベースにしており、誤りや改善点があればぜひ教えてください。

第0章:2次方程式が「よく分からない」あなたへ
「公式は覚えているのに、テストでは点が取れない……」
「平方完成? 因数分解? 結局どれを使えばいいのか分からない……」
「途中式のどこで間違えたのか分からなくなる……」
――そんな悩みを持つ高校生は、とても多いです。
「二次方程式って“3つの解き方がある”って言うけどさ……
どれを選べばいいのか、さっぱり分からないんだよなぁ……」
「大丈夫。今日は、『二次方程式の3つの解法をどう選ぶか』を
はっきり分かるように授業するわね。
“計算ができるようになる”だけじゃなく、どの方法を使えばラクになるのかまで見えるようになるから安心して。」
今日のゴール
- 因数分解・平方完成・解の公式の違いが分かる
- 式の形を見て、どの解法を選ぶか判断できる
- 入試レベルの問題でも、「とりあえず何をすればいいか」が見えるようになる
この記事の最後には、悪もこあい先生が「入試レベル」の挑戦問題を出します。
自分の力試しと思って、ぜひ最後までチャレンジしてみてくださいね。
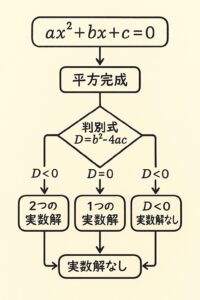
第1章:2次方程式の「解法の選び方チャート」
2次方程式
\( ax^2 + bx + c = 0 \)
には、3つの代表的な解き方があります。
- ① 因数分解
- ② 平方完成
- ③ 解の公式
どれを使っても正しく解けますが、テストでは「最速で・ミス少なく」解くことが大切です。
そのためには、式の形を見て「解き方を選ぶ」ことが必要になります。
解法の選び方:テキストチャート版
STEP1:
\(c = 0\) のときまず定数項 \(c\) を見る
- → 因数分解が最速(一発で解ける)
例:\( x^2 – 5x = 0 \Rightarrow x(x – 5) = 0 \Rightarrow x = 0, 5 \)
STEP2:\(a, b, c\) が小さい整数のとき
- 係数がすべて 1〜9 の小さな数字
- \(b\) と \(c\) の組み合わせで「因数」が作れそう
→ 因数分解を試す価値が高い
STEP3:\(b\) が偶数のとき
平方完成は b ÷ 2 を使うので、b が偶数のときは計算がとても楽になります。
→ 平方完成と相性が良い
STEP4:因数が作れない・係数が複雑なとき
- 係数が大きい・分数が多い
- 因数分解できるか判断しづらい
→ 解の公式を使うのが最も安全で確実です。
STEP5:判別式 \(D = b^2 – 4ac\) で「解の種類」を知る
-
- \(D > 0\):実数解が2つ
- \(D = 0\):実数解が1つ(重解)
- \(D < 0\):虚数解(グラフは x 軸と交わらない)
※虚数解の詳しい内容は、高校2年の「複素数と方程式」で学びます。
判別式を計算すると、「この式にどんな解があるのか」が一瞬で分かります。
解の公式を使うときには、先に D を計算しておくと全体の構造が見えやすくなります。
「二次方程式は “3つのどれでも解ける” けれど、
式の形に合わせて解法を選ぶと、ミスが劇的に減るのよ。」
第2章:因数分解で解けるタイプをマスターしよう
まずは最も軽量の方法、因数分解から。
数字が小さい、c が0、因数ペアが作れそう――こんな時に活躍します。

1. \(c = 0\) のときは「一瞬で解ける」
2次方程式
\( ax^2 + bx + c = 0 \) で、最初にチェックするのは \(c\) でした。
「え、なんで c を最初に見るの?」
「c が 0 のときは、
\( x(ax + b) = 0 \)
みたいに、“一瞬で解ける形”になるのよ。」
例:\( x^2 – 5x = 0 \Rightarrow x(x – 5) = 0 \Rightarrow x = 0, 5 \)
- 途中計算がほぼ不要
- ミスが少ない
- テストでの時間短縮に最適
2. 小さい整数が並んでいる式は「因数分解のチャンス」
係数が小さく、\(b, c\) の組み合わせで「掛けて c、足して b」になるペアが作れそうなら、
まず因数分解を疑ってみるのがコツです。
例題1:基本の因数分解タイプ
例題1:\( x^2 – 6x + 8 = 0 \)
「これは…… c が 8、b が -6。
掛けて 8、足して -6 になる数字を探すやつ!」
ステップ:
- 8 のペア → (1, 8), (2, 4)
- 足して -6 になるのは? → -2 と -4
よって
\( x^2 – 6x + 8 = (x – 2)(x – 4) = 0 \)
解は
\( x = 2, 4 \)
・b と c の符号をしっかり見る
・掛け算 → c / 足し算 → b の関係を書き出す
・ペアを全部書き出してから選ぶと、ミスが減るよ
つまずきポイント:符号がごちゃごちゃになる
「マイナスが混ざると、いつもどこかで間違うんだよなぁ……」
例:\( x^2 + x – 12 = 0 \)
c = -12 は「掛けて -12」になるペアを探す必要があります。
- (3, -4)
- (-3, 4)
- (6, -2)
- (-6, 2)
この中で、足して b = 1 になるのは
\(-3 + 4 = 1\)
なので
\( x^2 + x – 12 = (x – 3)(x + 4) = 0 \Rightarrow x = 3, -4 \)
「符号が複雑なときほど、“ペアを全部書く”のがミス防止のコツよ。」
練習問題(因数分解タイプ)
練習1:\( x^2 – 2x – 15 = 0 \)
ヒント:掛けて -15、足して -2 になるペアを探そう。
第3章:平方完成で「式を美しく整える」
平方完成は、二次式を
\( (x + p)^2 = q \)
というきれいな二乗の形に整えるテクニックです。
「平方完成って、途中でごちゃごちゃになって苦手なんだよなぁ……」
「実はね、平方完成は
b ÷ 2 を使うから、b が偶数のときが一番やりやすいのよ。」
平方完成の基本ステップ
例:\( x^2 + 6x + 5 = 0 \)
- \(x^2\) の係数が 1 か確認(今回は 1 なのでそのまま)
- x の係数 b = 6 を半分にする → 6 ÷ 2 = 3
- その数を二乗する → \(3^2 = 9\)
- 元の式に「9 を足して、9 を引く」
\( x^2 + 6x + 5 = x^2 + 6x + 9 – 9 + 5 \)
ここで、
\( x^2 + 6x + 9 = (x + 3)^2 \)
という “平方の形” ができます。
\( (x+3)^2 – 4 = 0 \Rightarrow (x+3)^2 = 4 \Rightarrow x+3 = \pm 2 \Rightarrow x = -1, -5 \)
「“足して引く”のところさえ理解できれば、むしろ公式よりミスが少ないの。」
「足して引く」って本当に意味あるの?
「“9 を足して 9 を引く”って、何の意味があるの?」
同じ数を足して、同じ数を引けば、式の値は変わりません。
そのうえで、「完全な平方」を作るために必要な分を足している、というイメージです。
図で考えると、足りない部分を“足して”正方形にし、余った分を“引いて”調整していると思うと分かりやすくなります。
(上の図解とセットで理解すると、平方完成のイメージがかなりクリアになります。)
b が奇数のときも手順は同じ
例:\( x^2 + 5x + 1 = 0 \)
5 ÷ 2 = 2.5、 \(2.5^2 = 6.25\)
\( x^2 + 5x + 1 = x^2 + 5x + 6.25 – 6.25 + 1 \)
\( (x+2.5)^2 – 5.25 = 0 \)

「b が奇数のときは途中で小数が出てくるけど、
手順は“b÷2 → 二乗 → 足す・引く”でいつも同じだよ。
ノートには途中式を縦にそろえて書くと、かなり見やすくなるよ。」
平方完成でミスしやすいポイント
- b を半分にするとき、符号を間違える
- 「足して引く」のうち、引くほうを書き忘れる
- 右辺に移項するときに符号が反転するのを忘れる
- x² の係数が1でないときに、最初の割り算を省略してしまう
練習問題(平方完成タイプ)
練習2:\( x^2 – 4x – 1 = 0 \)
ヒント:b÷2 = -2、\((-2)^2 = 4\)。
第4章:解の公式と判別式で「どんな式でも」解く
2次方程式の最終兵器が、解の公式です。
\( ax^2 + bx + c = 0 \) の解は
\( x = \dfrac{-b \pm \sqrt{b^2 – 4ac}}{2a} \)
「公式は覚えてるけど……判別式って、何のためにあるんだっけ?」
「判別式は、“解が何個あるか”が一瞬で分かる魔法の数字よ。」
判別式 D = b² − 4ac の意味
\( D = b^2 – 4ac \)
- D > 0 …… 実数解が 2 つ
- D = 0 …… 実数解が 1 つ(重解)
- D < 0 …… 実数解なし(虚数解)
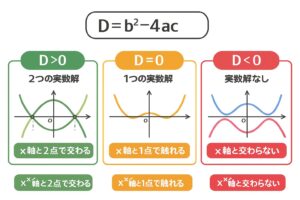
グラフで考えると、
- D > 0 …… 放物線が x 軸と2点で交わる
- D = 0 …… x 軸にちょうど接する
- D < 0 …… x 軸と交わらない
二次関数の単元(高校数学④)とも深くつながる部分です。
解の公式でミスしやすいポイント
- -b の符号を逆にし忘れる(b = -7 なら -b = 7)
- b² の符号をそのまま入れてしまう(-5² = -25 ではなく、(-5)² = 25)
- 分母 2a を書き忘れる(±の両方に 2a がかかる)
- すべてが偶数のときに、最初に全体を割って簡単にするのを忘れる
例題:公式で解くのが最速なタイプ
例題:\( 3x^2 – 2x – 7 = 0 \)
因数分解も平方完成もできますが、計算がかなり面倒なタイプです。ここでは公式で一気に解きます。
\( D = (-2)^2 – 4\cdot3\cdot(-7) = 4 + 84 = 88 \)
\( x = \dfrac{-(-2) \pm \sqrt{88}}{2\cdot3} = \dfrac{2 \pm \sqrt{88}}{6} \)
\( \sqrt{88} = \sqrt{4\cdot22} = 2\sqrt{22} \)
\( x = \dfrac{2 \pm 2\sqrt{22}}{6} = \dfrac{1 \pm \sqrt{22}}{3} \)
「公式を使うときは、先に D を計算しておいてから代入すると、
全体の構造が見えやすくなってミスが減るよ。」
平方完成でも解いてみる(少し重め)
例:\( 2x^2 – 5x – 3 = 0 \Rightarrow x^2 – \dfrac{5}{2}x – \dfrac{3}{2} = 0 \)
b ÷ 2 = -5/4, \((-5/4)^2 = 25/16\)
\( x^2 – \dfrac{5}{2}x + \dfrac{25}{16} = \dfrac{49}{16} \)
\( \left(x – \dfrac{5}{4}\right)^2 = \dfrac{49}{16} \Rightarrow x = \dfrac{5}{4} \pm \dfrac{7}{4} \)
\( x = 3,\ -\dfrac{1}{2} \)
※ 因数分解や公式の結果と一致しており、別の視点から同じ解にたどりつけることが分かります。
第5章:練習問題3問で「解法の選び方」を定着させよう
ここからは、実戦形式で3問だけ解いてみましょう。
どの問題も、「どの解法を選ぶか」がポイントです。
「よーし、さっき習った“解法の選び方”を試してみるぞ!」
練習問題①(因数分解タイプ)
\( x^2 – 2x – 15 = 0 \)
ヒント:c = -15、b = -2。掛けて -15、足して -2。
練習問題②(平方完成タイプ)
\( x^2 – 4x – 1 = 0 \)
ヒント:b が偶数(-4)なので、平方完成と相性がよいタイプです。
練習問題③(公式タイプ)
\( 3x^2 – 2x – 7 = 0 \)
ヒント:係数が複雑。因数分解するより公式のほうが安全です。
「たぶん解けた……けど、合ってるか不安だ……!」
練習問題の解答
練習①の解答
\( x^2 – 2x – 15 = 0 \)
掛けて -15、足して -2 → (-5, 3)
\( x^2 – 2x – 15 = (x – 5)(x + 3) = 0 \Rightarrow x = 5, -3 \)
練習②の解答
\( x^2 – 4x – 1 = 0 \)
\( x^2 – 4x + 4 – 4 – 1 = (x – 2)^2 – 5 = 0 \)
\( (x – 2)^2 = 5 \Rightarrow x – 2 = \pm\sqrt{5} \Rightarrow x = 2 \pm \sqrt{5} \)
練習③の解答
\( 3x^2 – 2x – 7 = 0 \)
\( D = (-2)^2 – 4\cdot3\cdot(-7) = 88 \)
\( x = \dfrac{1 \pm \sqrt{22}}{3} \)
「おお……!3問ともできた!
なんか、“二次方程式の壁”を少し越えられた気がする!」
第6章:悪もこあい先生の「入試レベル挑戦問題」
静かな教室に、コツコツとヒールの音が響く。
振り返ると、黒いチョークを持った悪もこあい先生が立っていました。

「ふふ……ここまでは“ウォーミングアップ”。
次は本気の入試レベル問題をあげるわ。」
「え、えぇぇ……もう少し優しいのは……」
「甘えないの。
解法を選べる力をつけてこそ、高校数学③の卒業よ。
さあ、解いてみなさい。」
入試レベル挑戦問題
\( 2x^2 – 5x – 3 = 0 \)
ヒント:
- 因数分解も可能だが、少しテクニックが必要
- 平方完成でも解けるが、途中が長い
- 公式なら確実に解ける
「b が -5 で、c が -3……。
因数分解もできそうだけど、ここは公式で行くべきか……?」
解答プロセス:3つの解法で比べてみよう
※この問題は第4章でも扱ったものです。同じ問題を3つの解法で比べてみましょう。
① 因数分解で挑戦
\( 2x^2 – 5x – 3 = 0 \)
ac 法:a×c = -6 → 掛けて -6、足して -5 → (-6, 1)
\( 2x^2 – 6x + x – 3 = 2x(x – 3) + 1(x – 3) = (2x + 1)(x – 3) \)
\( (2x + 1)(x – 3) = 0 \Rightarrow x = -\dfrac{1}{2},\ 3 \)
② 平方完成で挑戦(やや計算重め)
\( 2x^2 – 5x – 3 = 0 \Rightarrow x^2 – \dfrac{5}{2}x – \dfrac{3}{2} = 0 \)
b ÷ 2 = -5/4, \((-5/4)^2 = 25/16\)
\( x^2 – \dfrac{5}{2}x + \dfrac{25}{16} = \dfrac{49}{16} \)
\( \left(x – \dfrac{5}{4}\right)^2 = \dfrac{49}{16} \Rightarrow x = \dfrac{5}{4} \pm \dfrac{7}{4} \Rightarrow x = 3,\ -\dfrac{1}{2} \)
※ 因数分解や公式の結果と一致しています。
③ 解の公式で一撃
\( x = \dfrac{-(-5) \pm \sqrt{(-5)^2 – 4\cdot2\cdot(-3)}}{2\cdot2} = \dfrac{5 \pm \sqrt{25 + 24}}{4} = \dfrac{5 \pm \sqrt{49}}{4} \)
\( x = \dfrac{5 \pm 7}{4} \Rightarrow x = 3,\ -\dfrac{1}{2} \)
答え:\( x = 3,\ -\dfrac{1}{2} \)
「合格。
ちゃんと“解法を選ぶ力”がついてきているわね。
でも――ここからが本当のスタートよ。」
悪もこあい先生は、黒板に新しくこう書きます。
\( y = ax^2 + bx + c \)
「次は、二次関数。
放物線が見えるようにならないと、“二次方程式を理解した”とは言えないのよ。」
第7章:今回のまとめ + 高校数学シリーズ案内
「ここまで本当によく頑張りました。
今日の授業で、二次方程式は“3つの解法を使い分けるもの”だという感覚が、少しつかめたはずです。」
この記事で身についた力
1. 解法を「選ぶ」力
- \(c = 0\) → 因数分解
- \(b\) が偶数 → 平方完成
- 係数が複雑 → 解の公式
- 小さい整数 → 因数分解を試してみる
- 判別式 D → 解の種類が一瞬で分かる
2. 計算を整理して進める力
- 因数のペアを書き出す
- b÷2 → 二乗 → 足す・引く を順番に書く
- 公式は、先に D を計算してから代入する
「ノートが整理されてくると、ミスも減るし復習もしやすくなるよ。
その積み重ねが、テスト前の安心感につながるんだよね。」
3. 入試レベルの問題も「怖くない」感覚
- どの解法でもゴールにたどりつける
- 迷ったら公式でOK、という安全策を持てる
- 解法を比べることで「自分の得意パターン」も見えてくる
次のステップ:高校数学④ 二次関数へ
「次のステップは、二次関数です。
\( y = ax^2 + bx + c \) のグラフが、どんな形で、どこを通るのか。
放物線が“見える”ようになると、二次方程式の理解もぐっと深まりますよ。」
高校数学④では、放物線の基本形・軸・頂点・グラフの性質を扱う予定です。
ゆっくりとシリーズを進めていきますので、気長に待っていてくださいね。
高校数学シリーズ(①〜③+④案内)
- ⭐ 【高校数学①】多項式の展開をゼロから理解する|中学→高校へのつまずきが消える入門ガイド
- 高校数学②:因数分解の逆・展開の理解
- 高校数学③:2次方程式の解法(本記事)
- 高校数学④:二次関数が苦手な人へ
もこあい先生より:
今日の“なんで?”を大切にしよう。
正解より、考えた道のりが宝もの。
訂正と追記
本記事の内容に誤りや分かりにくい箇所があれば、お知らせいただけるととても助かります。
必要に応じて、ここに訂正・追記の履歴を残していきます。
参考文献・出典
- 高校数学Iレベルの教科書内容に基づく、二次方程式および二次関数の標準的な解説。






