二次関数が苦手になる理由は、才能ではありません。
多くの場合、途中で不安になり、確認のしかたが分からなくなるだけです。

この記事では、二次関数を

  • 読める形に翻訳（平方完成）し
  • 最大・最小を事故らず決め
  • 最後に1分で止血（見直し）できる

ところまで、一本道で整理します。
長く見えても、迷子にならないように作っています。

※はじめに（クリックで開く）

この記事は「高校数学・二次関数の最初の入口」を、初学者向けにできるだけ丁寧にまとめたものです。
計算ミスや見落としは誰にでも起きます。記事内の表②（1分チェック）で、最後に必ず確認してください。

目次
  1. まず確認：どこで止まっていますか？
  2. 二次関数は「計算」ではなく「翻訳」です
  3. 表①：よくあるミス地図（ここで止血できる）
  4. 平方完成①：a＝1 の基本（まず安心）
  5. 平方完成②：a≠1 のとき（ここが一番の壁）
  6. AIを使って練習する（本文を邪魔しない：detailsで2つだけ）
  7. 最大・最小は「候補を拾うだけ」です
  8. 例題3：最大・最小（範囲あり／頂点が範囲外→端点チェック必須）
  9. 表②：1分チェック（ミスを止血する）
  10. まとめ：肝心な所はこれだけ

まず確認：どこで止まっていますか？

この章でできること：「自分が詰まりやすい地点」を先に特定できます。

  • 平方完成の途中で「合ってるか不安」になる
  • a≠1になると急に分からなくなる
  • 最大・最小で「頂点だけ見て」ミスする（端点チェック忘れ）

ひとつでも当てはまれば大丈夫。
この記事は、そのために作っています。

二次関数は「計算」ではなく「翻訳」です

この章でできること：平方完成のゴール（読める形）と、頂点・軸を一撃で理解できます。

二次関数の目的はシンプルです。
式を、読める形に翻訳すること。

最終的に読みたい形は、これだけです。

y = a(x - p)^2 + q
  • 頂点： (p, q)
  • 軸： x = p（左右対称の線）
  • a：上に開く/下に開く、広い/細い

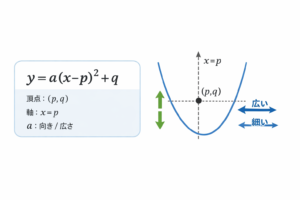
二次関数の頂点形y=a(x-p)^2+qを読み取り、頂点(p,q)と軸x=pおよびaの向きと広さの意味を整理した図
読むポイントは3つ：頂点(p,q)・軸x=p・aの向きと広さ
（つながり）a・p・qはグラフに何をする？（最小だけ）
  • a：符号で上/下、絶対値で広い/細い
  • p：左右に移動（頂点のx）
  • q：上下に移動（頂点のy）

※この続き（グラフの変化と見方）は、数学シリーズ⑤で扱います。

表①：よくあるミス地図（ここで止血できる）

この章でできること：「どの事故が起きやすいか」を先に知って、怖さを減らせます。

場面 ミスの型 具体例（ありがち） 原因 止血（最小手順）
平方完成（a=1） 足した分を戻し忘れ (x^2+4x+4) にしたのに外で −4 しない 「足す」と「戻す」がセットになっていない 中で足したら外で引くを声に出す
平方完成（a≠1） くくる前に平方完成して崩壊 2x^2+4x をそのまま平方に寄せる x^2の係数を無視 まずx^2の係数をくくる
平方完成（a≠1） 戻す量の係数ミス 2(x^2+2x+1) にしたのに −2 を忘れる 外側の係数が戻し量にもかかる 戻す量＝外の係数×足した数
頂点の読み取り 符号ミス（pの取り違え） y=a(x−2)^2+q を頂点(−2,q)とする （x−p）の形に慣れていない 頂点は(p,q)（pはそのまま）
最大・最小（範囲あり） 端点チェック忘れ 頂点だけ計算して終わる（頂点が範囲外） 候補を拾う意識がない 候補は頂点＋端点

この表は「間違い探し」ではなく、ミスを早く止めるための地図です。
例題中に「あ、これかも」と思ったら、該当の止血だけやればOK。

平方完成①：a＝1 の基本（まず安心）

この章でできること：平方完成の基本パターンを「翻訳」として実行できます。

例題1：

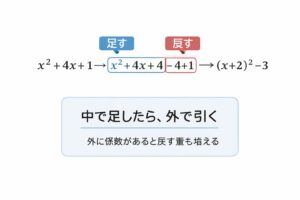
y = x^2 + 4x + 1

（色分け風）やることはこれだけです。

  • 平方を作るために：真ん中の係数4の半分は2 → 2の平方は4
  • 中で足したら：外で引いて戻す

y = x^2 + 4x + 1
  = (x^2 + 4x + 4) - 4 + 1
  = (x + 2)^2 - 3

ポイント：中で足した分（+4）は、必ず外で戻します（−4）。

平方完成で括弧の中に足した数を外で戻す手順を、足す地点と戻す地点が分かるように整理した図
「中で足す」→「外で戻す」をセットにする
（心理学ミニ）平方完成がつらいのは「頭が悪い」からではありません

平方完成がしんどい理由は、能力ではなく脳の作業台（ワーキングメモリ）の容量の問題です。
途中式では「符号」「足す」「戻す」など同時に持つ情報が増え、誰でも不安になります。

対策はシンプル。手順を固定して外に出すこと。
だからこの記事では、表①（ミス地図）と表②（1分チェック）で止血できるようにしています。

平方完成②：a≠1 のとき（ここが一番の壁）

この章でできること：a≠1でも崩れずに翻訳できます。

例題2：

y = 2x^2 + 4x + 1

最初に必ずやること： x^2 の係数をくくる


y = 2x^2 + 4x + 1
  = 2(x^2 + 2x) + 1

ここからは、( )の中だけ見ます。

  • 真ん中の係数2の半分は1 → 1の平方は1
  • 中で +1 したら、外では −1（外に2があるので戻す量は 2×1 = 2）

y = 2(x^2 + 2x) + 1
  = 2(x^2 + 2x + 1) - 2 + 1
  = 2(x + 1)^2 - 1
（コラム）健太の失敗：足した分を戻し忘れる

最大最小で候補を頂点と端点から拾い、頂点が範囲外なら端点のみを比較する流れを示した図
失敗していい。止血できれば伸びる。

健太：あれ？なんか答えが合わない…

もこあい先生：大丈夫。足した分を外で戻すのを忘れただけ。

（止血）「中で足したら、外で引く」をセットで。外に係数があるときは戻す量も増えるよ。

AIを使って練習する（本文を邪魔しない：detailsで2つだけ）

（AIプロンプト①）理解をやさしく確認したい 
あなたは高校数学の先生です。二次関数の平方完成を「翻訳」として説明してください。
ゴールは y=a(x-p)^2+q を読めるようにすることです。
a=1 と a≠1 の違い、足して戻す理由、軸 x=p と頂点(p,q)を短く整理し、
最後にチェック項目を5つだけ提示してください。

※AIの説明は誤りを含むことがあります。最後に必ずこの記事の表②（1分チェック）で確認してください。

（AIプロンプト②）追加の練習問題を作りたい（テスト用） 
二次関数の平方完成と最大・最小の練習問題を8問作ってください。
条件：
・平方完成（a=1）2問、（a≠1）2問
・最大最小（範囲ありで端点チェック必要）2問
・頂点と軸の読み取りだけ 2問
解答は折りたたみ形式で、最後に「表②の①〜⑤で確認する」導線を付けてください。

※AIの解答は間違うことがあります。必ず表②で自分で確認してください。

最大・最小は「候補を拾うだけ」です

この章でできること：最大・最小を「手順化」して事故を防げます。

最大・最小でやることは、基本これだけです。

  1. 頂点の値（翻訳して頂点(p,q)）
  2. 範囲があれば端点の値も計算
  3. 候補を比べて決める

※範囲（たとえば「0≦x≦3」）は 定義域。そのときに出てくる y の範囲が 値域 です。
値域は「候補を代入して一番大きい/小さい」を拾えば決まります。

（最小チェック）ラフ図を1回だけ描くなら、ここだけ見ればOK

  • ① 頂点は (p,q)
  • ② 軸は x=p
  • ③ aの符号で上/下
  • ④ 範囲（定義域）があるなら、頂点が範囲内か確認

ラフ図は芸術じゃありません。「候補がどれか」を確かめるための補助です。

平方完成の途中で健太が焦り、もこあい先生が足して戻す手順を示して落ち着かせる場面
最大・最小は「候補を拾って比べる」だけ

例題3：最大・最小（範囲あり／頂点が範囲外→端点チェック必須）

この章でできること：「頂点＋端点」で必ず決められます（頂点が範囲外なら端点だけ）。

問題：次の関数 y = (x - 3)^2 + 1 について、0≦x≦2 の範囲での最小値と最大値を求めよ。

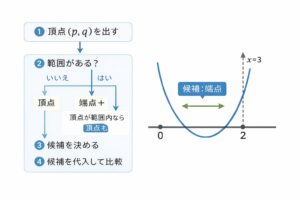
手順は固定：①頂点 → ②頂点が範囲内？ → ③候補を代入 → ④比較

① 翻訳（すでに頂点形）→ 頂点と軸

この式はすでに y=a(x-p)^2+q の形です。
a=1, p=3, q=1 なので、

  • 頂点：(3, 1)
  • 軸：x=3
  • a=1 なので上に開く（最小が出やすい）

② 頂点は範囲内か？（ここが事故ポイント）

今回の範囲は 0≦x≦2。
頂点のx座標は x=3 なので、範囲外です。

結論：頂点が範囲外なら、最大・最小は端点で決まります。

③ 候補（端点）を代入

候補は端点の2つだけ：x=0 と x=2


x=0 のとき
y = (0 - 3)^2 + 1
  = 9 + 1
  = 10

x=2 のとき
y = (2 - 3)^2 + 1
  = 1 + 1
  = 2

④ 比べて決める

  • 最小値：2（x=2 のとき）
  • 最大値：10（x=0 のとき）
（よくあるミス）頂点だけ見て「最小値は1」としてしまう

頂点は (3,1) なので「最小値は1」と言いたくなります。
でも、範囲は 0≦x≦2。x=3 は使えません。
だから、今回の最小値は 2 になります。

表②：1分チェック（ミスを止血する）

この章でできること：どんな問題でも「不安」を手順に戻せます。

チェック 見るところ よくある事故
① aの符号 上に開く/下に開く 最大・最小の方向を取り違える
② 頂点(p,q) y=a(x-p)^2+q に翻訳できたか pの符号ミス／翻訳未完了
③ 範囲（定義域） 0≦x≦3 など条件の有無 範囲を見落とす
④ 頂点は範囲内？ x=p が範囲に入るか 頂点が範囲外なのに頂点だけで決める
⑤ 候補漏れ 候補（頂点/端点）を全部代入 端点代入し忘れ／比較し忘れ

まとめ：肝心な所はこれだけ

  • 平方完成は翻訳：y=a(x-p)^2+q に直す
  • 頂点は(p,q)、軸はx=p
  • 最大・最小は候補拾い：頂点＋端点（範囲外なら端点）
  • 不安になったら表②（1分チェック）で止血

（今やること）表②の①〜⑤を、今の例題3で1回だけなぞってから終わり。

※この続き（グラフの変化と見方）は、数学シリーズ⑤で扱います。
今回は、翻訳（平方完成）と止血（表②）ができれば十分です。

不安になったら戻れる（数学の土台）

（おまけ）中学の文字式が不安な人へ

もこあい先生より：
「今日の“なんで？”を大切にしよう。正解より、考えた道のりが宝もの。」